Johannes Firzlaff, Department of Wood Technology, Fachhochschule Eberswalde

Foundations for Numerical Computation of
Notch Depths of Round Timber Shoulders

Preliminary Remark

This thesis is a revision of a lecture given on the occasion of an examination in the subject of Technical English. Although it is based on my German edition published "above" this page it is no translation.

To start with we should consider the

Shoulder and its Geometry

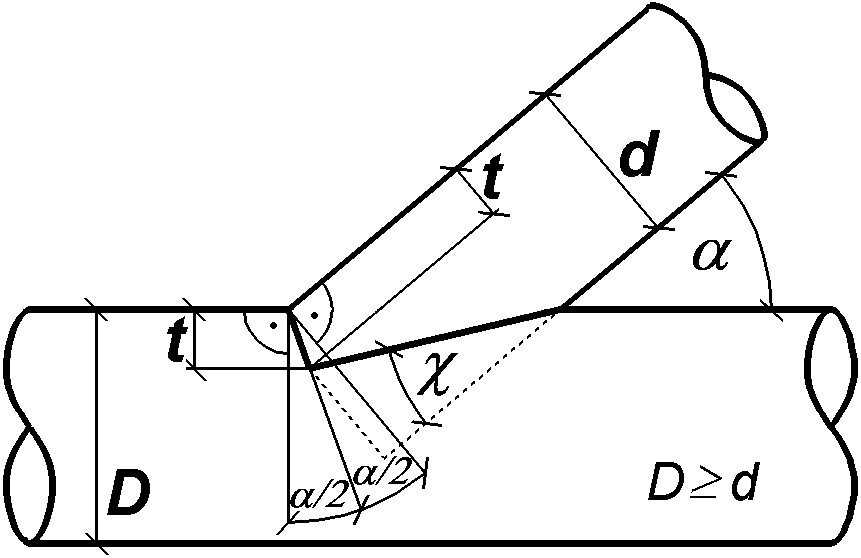
A shoulder is one possible carpenter´s joint of two wooden rods. It can only be used for compressive force transmission. The axis of the rod to be fixed is inclined to the axis of the incorporating rod.

The rod force F_alpha is divided up into two parts - shoulder force F_alpha/2 and bevel force F_chi - and transmitted by contact in two planes - shoulder plane A_alpha/2 and bevel plane A_chi.
The amount of the shoulder angle alpha/2 is given by the joint angle alpha. The bevel angle chi depends on the notch depth t: An increasing notch t decreases bevel angle chi.

Engineers should endeavour to keep notch depths as small as possible in order to reduce the weakening of the cross-section-area of incorporating rods. This is the motive for this thesis.

It is postulated: Contact surfaces without friction, exact fits and rigid bodies. The diameters of the incorporating rods must be at least as big as those of the rods which are to be fixed. Given that, the derivations can also be applied to incorporating squared timber instead of incorporating round timber.

Being an anisotropic material the strength of wood depends on the angle of grain to stress. Here the German standard DIN 1052 [1988] is used for determining the so called safe working stress.

Anything will be said about the allowed notch depth t and joint angle alpha, the length of safety-wood in front of the joint and the problem of the arrangement protection.

Study of Nexus, Strategy of Solution

The rod force F_alpha and the joint angle alpha are given. So the shoulder angle alpha/2 is also defined by the geometric definition of the shoulder. With this shoulder plane safe working stress sigma_{alpha/2 sws}and direction of shoulder force F_alpha/2 are determined. Shoulder force F_alpha/2 and shoulder plane A_alpha/2 must be perpendicular to each other because no friction is postulated.

Shoulder plane A_alpha/2 takes the form of a segment of an ellipse and is a function of notch depth t and joint angle alpha. The necessary area of the shoulder plane

sigma = F / A <=> A_alpha/2 = F_alpha/2 / sigma_{alpha/2 sws}

is calculated from the values of shoulder force F_alpha/2 and shoulder plane compressive safe working stress sigma_{alpha/2 sws}.

Quantity and orientation of the bevel plane A_chi, also shaped like an ellipse segment, and therefore the direction of the bevel force F_chi are functions of notch depth t as well. As above shoulder force F_alpha/2 also bevel force F_chi must be perpendicular to its pertinent plane.

But the direction of bevel force F_chi has also an influence on the quantity of shoulder force F_alpha/2! This is illustrated by the triangle of forces.

So each change of notch depth t does not only result in changes of bevel area A_chi and particularly shoulder area A_alpha/2, but also exercises an influence on the values of both components shoulder and bevel force F_alpha/2 and F_chi in which rod force F_alpha is to be dissected.

Consequently shoulder stress sigma_alpha/2 varies directly by corrections of notch depth t and indirectly as a feedback by change of value of shoulder force F_alpha/2 which ensue from notch depth t correction simultaneously.

Now then notch depth t has to be chosen to such a degree that this inequation

A_alpha/2 >= F_alpha/2 / sigma_{alpha/2 sws}

is served.

At the same time the bevel tension sigma _chi value must not overstep both safe working stresses sigma _{(90°-chi) sws} and sigma_{(90°-alpha+chi) sws} in the bevel plane A_chi which come up to different quantities on the side of the rod to be fixed and the incorporating rod. The difference of the quantities results from the different angles.

rod angle alpha rod force Falpha(look next figure) shoulder angle alpha/2 shoulder force Falpha/2(look next figure) bevel angle chi bevel force Fchi(look next figure) notch depth t diameter of the rod to be fixed d angle of grain to stress in shoulder plane alpha/2 angle of grain to stress in bevel plane of rod to be fixed 90°-chi angle of grain to stress in bevel plane of incorporating rod 90°-alpha+chi chi = arctan [ (d-t) / ( t*tan(alpha/2) + d/tan(alpha) ) ] Remark: shoulder and bevel plane form a right angle if chi = alpha/2.

Having done this preliminary work the route of solution is marked by the inequation above: Formula-derivations for the two components of rod force, safe working stresses and ellipse-segment areas.

The first point in the order just fixed is the

Rod Force and its Components

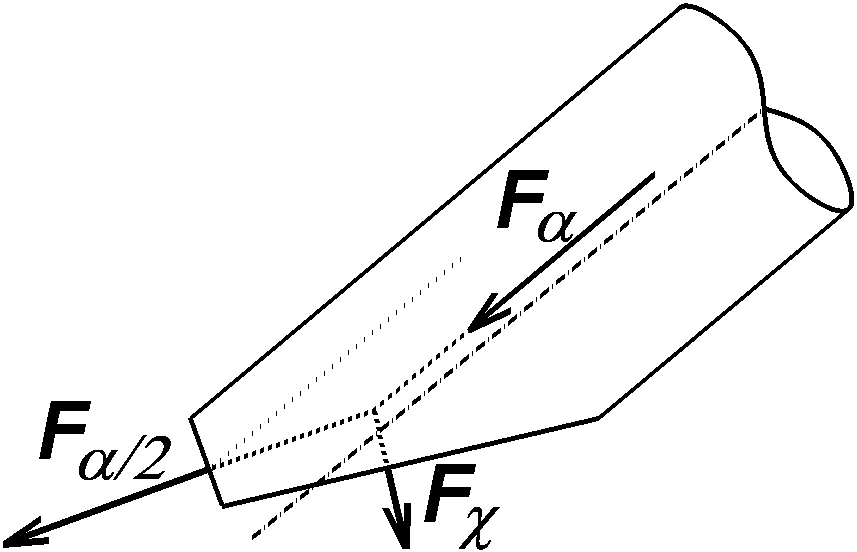Remark: Positive forces pull at the contact surfaces. The dissection of rod force Falpha into shoulder force Falpha/2 and bevel force Fchi results in the following triangle of forces after bevel force Fchi has been translated.

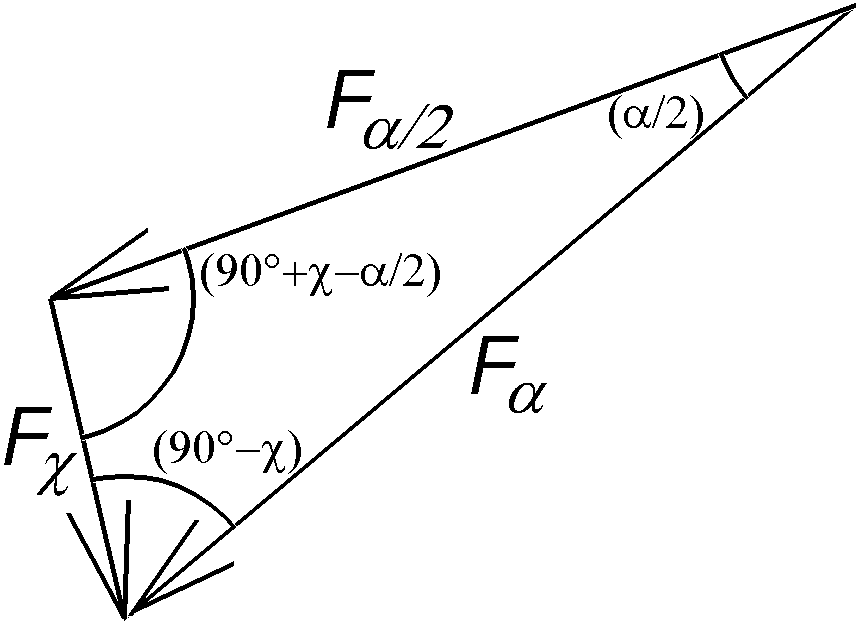The values of the components follow from the sine theorem: Falpha / sin(90°+chi-alpha/2) = Falpha/2 / sin(90°-chi) = Fchi / sin(alpha/2) <=> Falpha/2= Falpha*cos(chi)/ cos(chi-alpha/2) and Fchi = Falpha*sin(alpha/2) / cos(chi-alpha/2)

The next step is the

Calculation of Safe Working Stress at any Angle phi

As mentioned earlier here the formula according to German standard DIN 1052 [04.1988] is used. The compressive safe working stress by angle grain to wood phi sigma _{phi sws} is calculated from the compression strength parallel >(par)<to grain minus the difference strength perpendicular >(per)< to strength parallel to grain multiplied by sine of angle phi.

sigma _{phi sws} = sigma_{par sws} - (sigma_{par sws} - sigma_{per sws}) * sin(phi) ;
sigma_phi; sigma_par; sigma_per <= 0 (free from DIN 1052 T 1 [1988]

The last single point is the

Surface Calculation of Ellipse Segments (Shoulder and Bevel Plane)

An ellipse can be described as a projection of a circle on a inclined plane. In this case the circle corresponds to the cross-section and the ellipse to that shoulder plane of round timber which will follow from a notch depth t in size of diameter d.

While the length of the minor axis of the ellipse coincides with the round timber diameter the major axis assumes a value increased by the factor 1/cos(alpha/2).

Smaller notch depths (t < d) result in shoulder planes shaped like ellipse segments. These are projections of circle segments, prolate in one direction and perpendicular to the chord with the same factor 1/cos(alpha/2).

The circle segment area is calculated from two terms of a sum: The area of the circle sector reduced by two triangles which make the difference to a circle segment.

Circle-Segment:

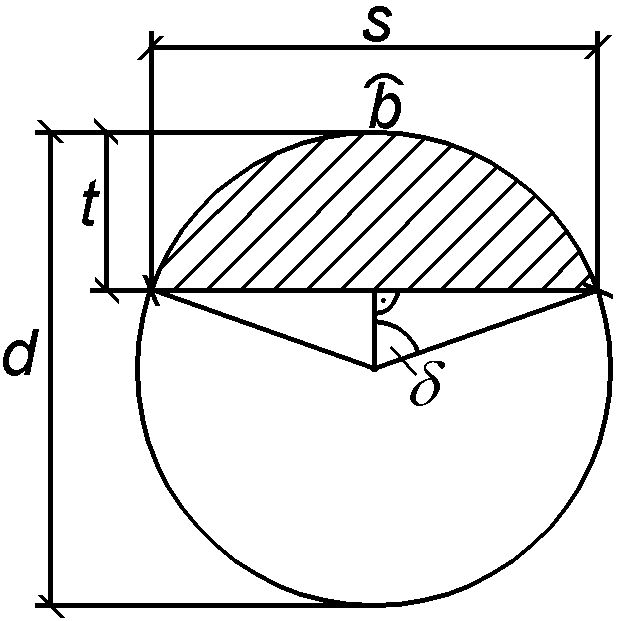s = 2*[ (d/2)^2 - ((d/2) - t)^2 ]^0,5 = 2*[d*t - t^2]^0,5 delta = (barc/2) / (d/2) <=> barc = d*delta = d*arccos[ ((d/2) - t) / (d/2) ] = d*arccos[ (d - 2*t)/d ] Acircle-segment"alpha/2" = ( d^2*pi*barc / (4*d*pi) ) - (d*t - t^2 )^0,5*((d/2) - t) = (1/4) * [ d^2*arccos( (d - 2*t)/d ) - 2*(d*t - t^2)^0,5*(d - 2*t) ] Ellipse-Segment: Aalpha/2 = [1/cos(alpha/2)]*Acircle-segment"alpha/2"

In bevel surface calculation A_chi alpha/2 is replaced by 90°-chi and t by d-t. The prolate factor changes to 1/sin(chi).

Now the individual results can be pooled in our point

Compilation of the Individual Studies

Notch depth t has to fulfill the following systems of inequations:

A_alpha/2 >= F_alpha/2 / sigma_{alpha/2 sws} and
A_chi >= F_chi / sigma_{(90°-chi) sws} and A_chi >= F_chi / sigma_{(90°-alpha+chi) sws} ;

in which

A_alpha/2 = (1 / (4*cos(alpha/2)) )*[ d^2*arccos( (d - 2*t)/d ) - 2*(d*t - t^2)^0,5*(d - 2*t) ]

A_chi = (1 / (4*sin(chi)) * [ d^2*arccos( (2*t - d)/d ) - 2*(d*t - t^2)^0,5*(2*t - d)]

F_alpha/2 = F_alpha*cos(chi) / cos(chi-alpha/2)

F_chi = F_alpha*sin(alpha/2) / cos(chi-alpha/2)

sigma _{alpha/2 sws} = sigma_{par sws} - (sigma_{par sws} - sigma_{per sws})*sin(alpha/2)

sigma _{(90°-chi) sws} = sigma_{par sws} - (sigma_{par sws} - sigma_{per sws})*cos(chi)

sigma _{(90°-alpha+chi) sws} = sigma_{par sws} - (sigma_{par sws} - sigma_{per sws})*cos(chi-alpha)

chi = arctan[ (d-t) / (t*tan(alpha/2) + d/tan(alpha)) ]

This system with its integral equations can be used to check notch depth t already given but not for expansion of a simple explicit notch depth formula. A second possibility of use is numerical calculation based on the computer. This facility shall be returned to after the résumé.

Résumé

In brief the shoulder and its geometric details as a carpenter´s joint of wooden rods were looked at.

Then the nexus was studied where theoretic and complex assumptions were made.

In anticipated consequence of the complicated function for calculating the contact areas the rod force was exactly dissected in its components since indeed the computer was intended for calculation anyway.

For safe working stress calculation the German standard DIN was applied. General formulae for each angle grain to stress could be retrieved by geometric analysis of the sketch.

Finally the function for contact areas was worked out of a prolate circle fragment.

The findings of the research is a system of inequations which can be used for numerical computation.

View of Eccentricity of Rod Force

First please have a look at the second sketch. The vectors F_alpha/2 and F_chi act on the centres of gravity of their respective planes in normal directions. These points are calculated in their distances to midline in cross-section by the formula

a = s³ / (12 * A).

For s and A the expressions from the circle-segment-calculation are to be applied. Then they are projected in rod direction into their respective planes. Finally the eccentricity of the rod force is constructed by graphic addition of the two vectors.

The analytic determination of the resultant-position with the model introduced here seems to become very complicated. Moreover it must be noticed to be on the unreliable side by doing so because of the idealized hypothesises.
This is illustrated in the above mentioned sketch: The thinnest dotted line shows the result of eccentricity determination according to the ordinary principle:
Dissection of rod force only in shoulder plane in

normal force F_{alpha/2 N} = F_alpha * cos(alpha/2) and
transverse force F_{alpha/2 T} = F_alpha * sin(alpha/2).

However I would like to point out that my method is qualified just for round timber, too: Notches with depths as deep as their rod-to-be-fixed-diameters produce bevel plane areas of nought!

Thanks

I express my thanks to Mr Strey, Fachhochschule Neubrandenburg, for checking (the mathematical part of) this thesis.
Furthermore I thank Mr Dietterle and Mr Bonadt, our specialists in information technology, for their patient help in the multitude of problems I got in preparation of this presentation.

Application

The work presented here is applied to a MICROSOFT EXCEL^© 7 file. With this application notch depths t, diameters d and rod forces F_alpha can be tested for accomplishment of the inequation system without any nomogram and furthermore automatically optimized by mouseclick. It is published on the internet "besides" these "foundations".

Click here to have opportunity to get an impression of this program. It is only available in German language.

All Rights Reserved

I reserve all rights to this thesis and to the computer program. For propagation (and further propagation) in printed media my permission is needed.

For use of my program it is necessary to read and understand the German version of this thesis and the German instructions for use.

Eberswalde, Campus Möller-Straße, 10.09.1997 (10th September 1997) (Grammatical and stylistic revision on 13th November 1997) Johannes Firzlaff

Survey of my themes

Homepage of my Fachhochschule Eberswalde