Johannes Firzlaff, Student der Holztechnik, Fachhochschule Eberswalde
Praktikant im zweiten praktischen Semester (SS1996) im
RECONTIE^®Ingenieurbüro-Holz-GmbH, Berliner Straße 5, 13127 Berlin-Buchholz

Grundlagen zur numerischen Berechnung der
Versatztiefen bei Rundholz-Stirnversätzen

Eberswalde, 31.07.1996 - Überarbeitung 20.12.1996

Vorgeschichte und Inhalt

Im Rahmen meines zweiten praktischen Semesters hatte ich die Aufgabe, für eine Rundholz-Fachwerkbrücke die erforderlichen Stirnversatztiefen der Verbindungen zu berechnen. Da keine Bemessungsformeln bekannt waren, entwickelte ich eine eigene Theorie.
Die Brücke wurde letztlich mit Knotenblechen geplant. Auch fand man noch Literatur zum Versatzproblem. Unabhängig davon möchte ich hier das Ergebnis der eigenen Arbeit vorstellen.

In dieser Arbeit werden reibungsfreie Berührflächen, ideale Paßflächen und starre Körper angenommen. Der Durchmesser des aufnehmenden Rundholzes darf nicht kleiner als der des aufzunehmenden Rundholzes sein. Damit gelten die Berechnungen auch für in Kantholz einversatzte Rundhölzer.

Nicht eingegangen wird auf den Stirnversatz als solchen, die zulässige Versatztiefe, den zulässigen Versatzwinkel und die Frage der Lagesicherung. Auch werden keine Flächenverluste durch Verbindungen, zum Beispiel Zapfen, von aufnehmenden und aufzunehmenden Rundholz berücksichtigt.

Betrachtung der Zusammenhänge, Lösungsansatz

Die Stabkraft F_alphaund der Versatzwinkel alpha sind vorgegeben. Mit der geometrischen Definition des Stirnversatzes ist so auch der Stirnwinkel alpha/2 festgelegt. Damit sind gleichfalls die zulässige Stirnspannung sigma_alpha/2 und die Richtung der Stirnkraft F_alpha/2 eindeutig bestimmt.

Die die Form eines Ellipsenabschnittes annehmende Stirnfläche A_alpha/2 ist eine Funktion der Versatztiefe t und des Versatzwinkels alpha. Die erforderliche Stirnfläche errechnet sich nach

sigma = F / A <=> A_alpha/2 = F_alpha/2 / sigma_{alpha/2 zul}

aus den Beträgen der Stirnkraft und der zulässigen Stirnspannung. Betrag und Lage der ebenfalls ellipsenabschnittförmigen Schmiegefläche A_chi und so auch der Richtung der Schmiegekraft F_chi sind gleichfalls Funktionen der Versatztiefe.

Jede Änderung der Versatztiefe bewirkt also nicht nur Änderungen der Schmiegefläche und insbesondere der Stirnfläche, sondern beeinflußt auch die Beträge der Komponenten Stirn- und Schmiegekraft, in welche die Stabkraft zu zerlegen ist.
Die Stirnspannungen ändern sich also direkt durch Korrekturen an den Versatztiefen und indirekt als Rückkopplungseffekt durch die gleichzeitig erfolgenden Änderungen der Stirnkraft-Beträge.
Die Versatztiefe muß nun so gewählt werden, daß die Ungleichung

A_alpha/2 >= F_alpha/2 / sigma_{alpha/2 zul}

erfüllt wird.

Gleichzeitig darf der Betrag der an der Berührfläche der Schmiegeebenen auftretenden Schmiegespannung die auf der aufnehmenden und aufzunehmenden Seite unterschiedlich großen Beträge der zulässigen Spannungen, sigma_{(90°-alpha+chi) zul} und sigma _{(90°-chi) zul} , nicht überschreiten. Druckspannungen werden mit negativen Vorzeichen angegeben.

Geometrische Betrachtungen, Skizzen, Berechnung von Stab- und Schmiegekraft

Versatzwinkel alpha Stabkraft Falpha Stirnwinkel alpha/2 Stirnkraft Falpha/2 Schmiegewinkel chi Schmiegekraft Fchi Versatztiefe t Durchmesser des zuversatzenden Stabes d Belastungswinkel zur Faser in der Stirnfläche alpha/2 Belastungswinkel zur Faser in der Schmiegefläche des zu versatzenden Stabes 90°-chi Belastungswinkel zur Faser in der Schmiegefläche des versetzenden Stabes 90°-alpha+chi chi = arctan [ (d-t) / ( t*tan(alpha/2) + d/tan(alpha) ) ]

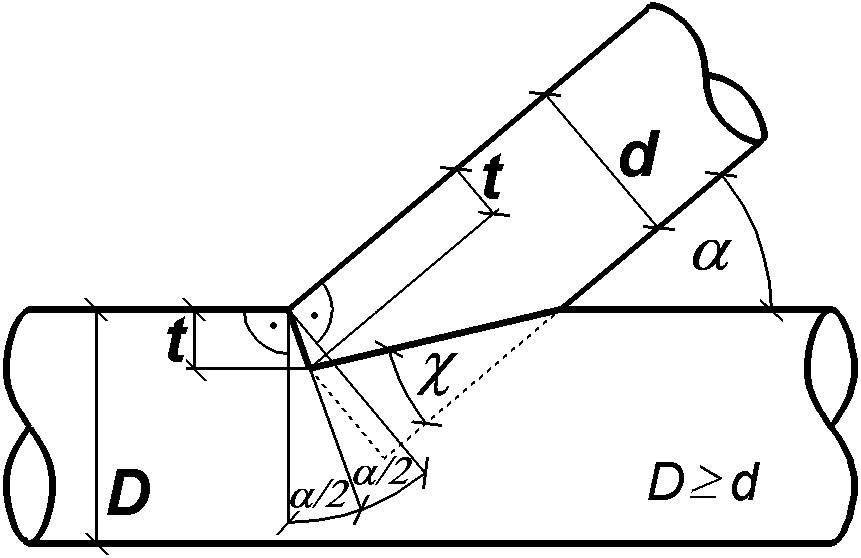Hinweis: Stirn- und Schmiegefläche bilden einen rechten Winkel, wenn chi = alpha/2.

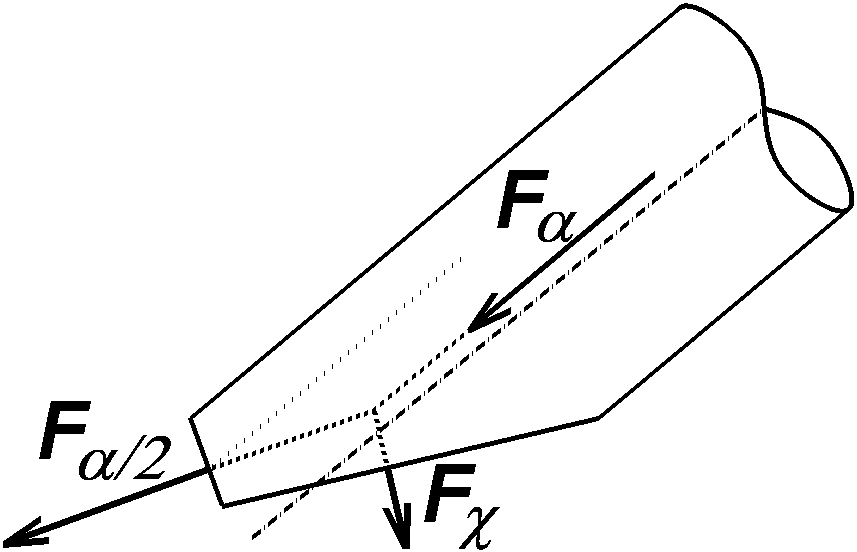Hinweis: Positive Kräfte ziehen an den Versatzflächen. Die Zerlegung der Stabkraft Falpha in die Stirnkraft Falpha/2 und Schmiegekraft Fchi führt nach Parallelverschiebung der letzteren zum abgebildeten Kraftdreieck

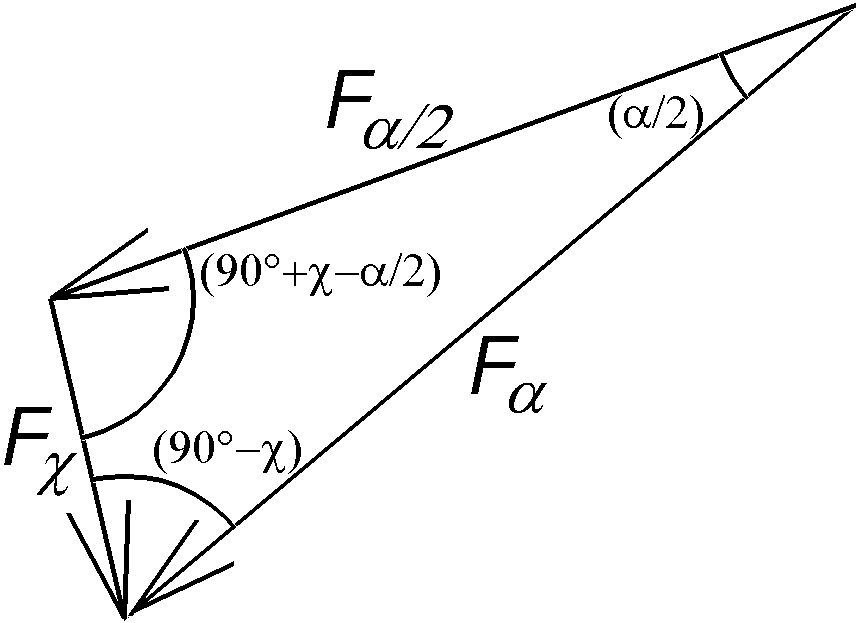Nach dem Sinussatz gilt Falpha / sin(90°+chi-alpha/2) = Falpha/2 / sin(90°-chi) = Fchi / sin(alpha/2) <=> Falpha/2= Falpha*cos(chi)/ cos(chi-alpha/2) und Fchi = Falpha*sin(alpha/2) / cos(chi-alpha/2)

Berechnung der zulässigen (Druck-)Spannungen bei beliebigem Faser-Last-Winkel phi

sigma _{phi zul} = sigma_{par zul} - (sigma_{par zul} - sigma_{senk zul}) * sin(phi) ; sigma_phi; sigma_par; sigma_senk >= 0 (frei nach DIN 1052 T 1 [1988]

Berrechnung der Ellipsenabschnitte (Stirn- und Schmiegefläche)

Beschreiben kann man die Ellipse als Bild eines Kreises auf einer zu ihm schiefen Ebene. Hier entspricht der Kreis dem Querschnitt und die Ellipse der Stirnfläche des Rundholzes, die man bei einer Versatztiefe t in Höhe des Durchmessers d erhalten würde.

Während die Nebenachse der Ellipse in ihrer Länge dem Durchmesser des Rundholzes entspricht, nimmt die Hauptachse einen um den Faktor 1/cos(alpha/2) höheren Wert ein. Geringere Versatztiefen (t<d) führen zu Ellipsenabschnitt-förmigen Stirnflächen. Diese sind Bilder von Kreisabschnitten, gestreckt in einer Richtung und senkrecht zur Sehne mit demselben Faktor 1/cos(alpha/2).

Kreisabschnitt:

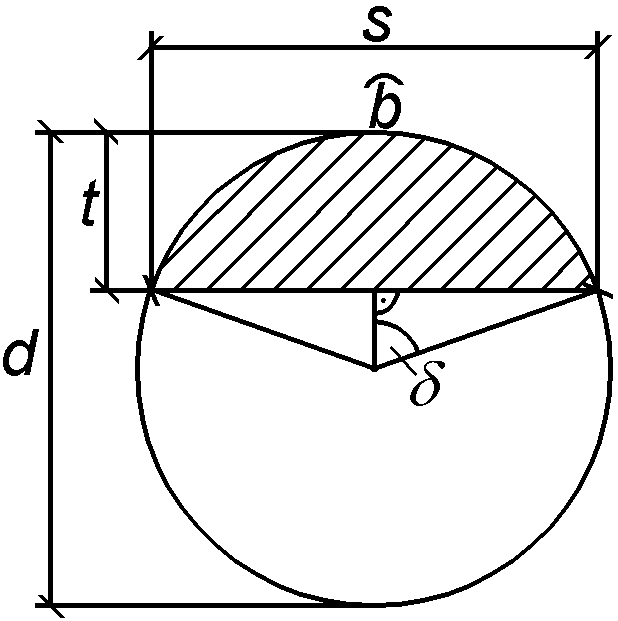s = 2*[ (d/2)^2 - ((d/2) - t)^2 ]^0,5 = 2*[d*t - t^2]^0,5 delta = (bBogen/2) / (d/2) <=> bBogen = d*delta = d*arccos[ ((d/2) - t) / (d/2) ] = d*arccos[ (d - 2*t)/d ] AKreisabschnitt"alpha/2" = ( d^2*pi*bBogen / (4*d*pi) ) - (d*t - t^2 )^0,5*((d/2) - t) = (1/4) * [ d^2*arccos( (d - 2*t)/d ) - 2*(d*t - t^2)^0,5*(d - 2*t) ] Nun Ellipsenabschnitt: Aalpha/2 = [1/cos(alpha/2)]*AKreisabschnitt"alpha/2"

Bei der Berechnung der Schmiegefläche A_chi werden alpha/2 durch 90°-chi und t durch d-t ersetzt. Der Streckfaktor ändert sich zu 1/sin(chi)

Zusammenführung der einzelnen Betrachtungen

Die Versatztiefe t muß nun als notwendige Bedingung folgendes Ungleichungssystem erfüllen:

A_alpha/2 >= F_alpha/2 / sigma_{alpha/2 zul} und A_chi >= F_chi / sigma_{(90°-chi) zul} und A_chi >= F_chi / sigma_{(90°-alpha+chi) zul} ; wobei

A_alpha/2 = (1 / (4*cos(alpha/2)) )*[ d^2*arccos( (d - 2*t)/d ) - 2*(d*t - t^2)^0,5*(d - 2*t) ]

A_chi = (1 / (4*sin(chi)) * [ d^2*arccos( (2*t - d)/d ) - 2*(d*t - t^2)^0,5*(2*t - d)]

F_alpha/2 = F_alpha*cos(chi) / cos(chi-alpha/2)

F_chi = F_alpha*sin(alpha/2) / cos(chi-alpha/2)

sigma _{alpha/2 zul} = sigma_{par zul} - (sigma_{par zul} - sigma_{senk zul})*sin(alpha/2)

sigma _{(90°-chi) zul} = sigma_{par zul} - (sigma_{par zul} - sigma_{senk zul})*cos(chi)

sigma _{(90°-alpha+chi) zul} = sigma_{par zul} - (sigma_{par zul} - sigma_{senk zul})*cos(chi-alpha)

chi = arctan[ (d-t) / (t*tan(alpha/2) + d/tan(alpha)) ]

Schlußbemerkung und Ansatz zur Berechnung der Ausmittigkeit

In dieser Arbeit wurden theoretische und aufwendige Annahmen getroffen. Die Entwicklung einer einfachen expliziten Formel für die Versatztiefe war wegen der Schwierigkeiten in den Flächenberechnungen von Anfang an ausgeschlossen. Deshalb wurde auch die Stabkraft aufwendig und exakt in ihre Komponenten zerlegt, da für die Berechnungen ohnehin der Computer vorgesehen ist.

Zur Berechnung der Ausmittigkeit verweise ich zunächst auf die mittlere Skizze der zweiten Seite. Die Vektoren F_alpha/2 und F_chi greifen (in Normal-Richtung) an den Schwerpunkten der jeweiligen Versatzflächen an. Diese Punkte sind nach

Bartsch, Taschenbuch mathematischer Formeln mit a = s^3 / (12*A_KrAb)

in ihren Abständen a in der Queraschnittsebenen zur Stab-Mittellinie berechnet und dann in Stabrichtung in die Versatzebenen projiziert. Dabei sind für s und A die Ausdrücke aus der Kreisabschnittsberechnung einzusetzten. Die Ausmittigkeit der resultierenden Stabkraft F_alpha ist dann graphisch konstruiert worden.

Die analytische Lage-Ermittlung der Resultierenden im hier vorgestellten Modell droht sehr kompliziert zu werden. Außerdem wird man wegen der idealisierten Annahmen sehr auf der unsicheren Seite liegen. Veranschaulicht wird dieses in der genannten Zeichnung: Die schwächste Punktlinie zeigt das Ergebnis der Ausmittigkeits-Bestimmung nach dem wohl üblichen Prinzip, die Stabkraft nur in der Stirnfläche in eine
Normalkraft F_{alpha/2 N} = F_alpha*cos(alpha/2) und eine
Querkraft F_{alpha/2 Q} = F_alpha*sin(alpha/2) zu zerlegen.

Ich möchte aber an dieser Stelle darauf hinweisen, daß gerade bei Rundholz meine Methode auch ihre Berechtigung hat; denn bei den Stabdurchmessern entsprechenden Versatztiefen betragen die Schmiegeflächen Null!

Dank

Ich danke Herrn Strey, Fachhochschule Neubrandenburg, für die Durchsicht der Arbeit.
Außerdem danke ich den Herren Dietterle und Bonadt, unsere IT-Fachleute, für die geduldige Hilfe in der Vielzahl von Problemen, die bei der Anfertigung dieser Präsentation entstanden sind.

Anwendung

Die vorgestellten Erkenntnisse habe ich in eine Computer-Datei des Tabellenkalkulation-Programmes Excel^© 7 umgesetzt. Mit dieser Anwendung können neben den Versatztiefen t auch die Durchmesser d und die Stabkräfte F_alpha ohne Nomogramm auf Erfüllung des Ungleichungssystems geprüft und auch per Mausklick automatisch optimiert werden. Die Veröffentlichung ist hier "unter" dieser Arbeit erfolgt. Hier ist eine Musteransicht.

Vorbehalt

Ich behalte mir alle Rechte an dieser Arbeit und an dem Computer-Programm vor. Verbreitung (und Weiterverbreitung) in Print-Medien nur mit meiner Erlaubnis.

Eberswalde, Campus Möller-Straße, 17.02.1997 Johannes Firzlaff

Hinweis: Zum Ausdrucken empfehle ich eine der "doc-Dateien" dieser Arbeit.
Clicken Sie bitte genau diesen Link. 

Zur Homepage meiner Fachhochschule Eberswalde